Bharatiya Sanskriti Ke Vikas Me Jain Vangamay Ka Avdan Part 02

SR No.: 032458
Original Sutra Author: N/A
Author: Nemichandra Shastri, Rajaram Jain, Devendrakumar Shastri
Publisher: Prachya Shraman Bharati
Publication Year: 2003
Total Pages: 478
Language: Hindi
Classification: Book_Devnagari
File Size: 13 MB

Page 427

३८२
भारतीय संस्कृति के विकासमें न वाङ्मयका अवदान
amongss these three great writers, and yet those of mahavirachaya art much belter then the one to be found in either Brahmagupta or Bhaskara.
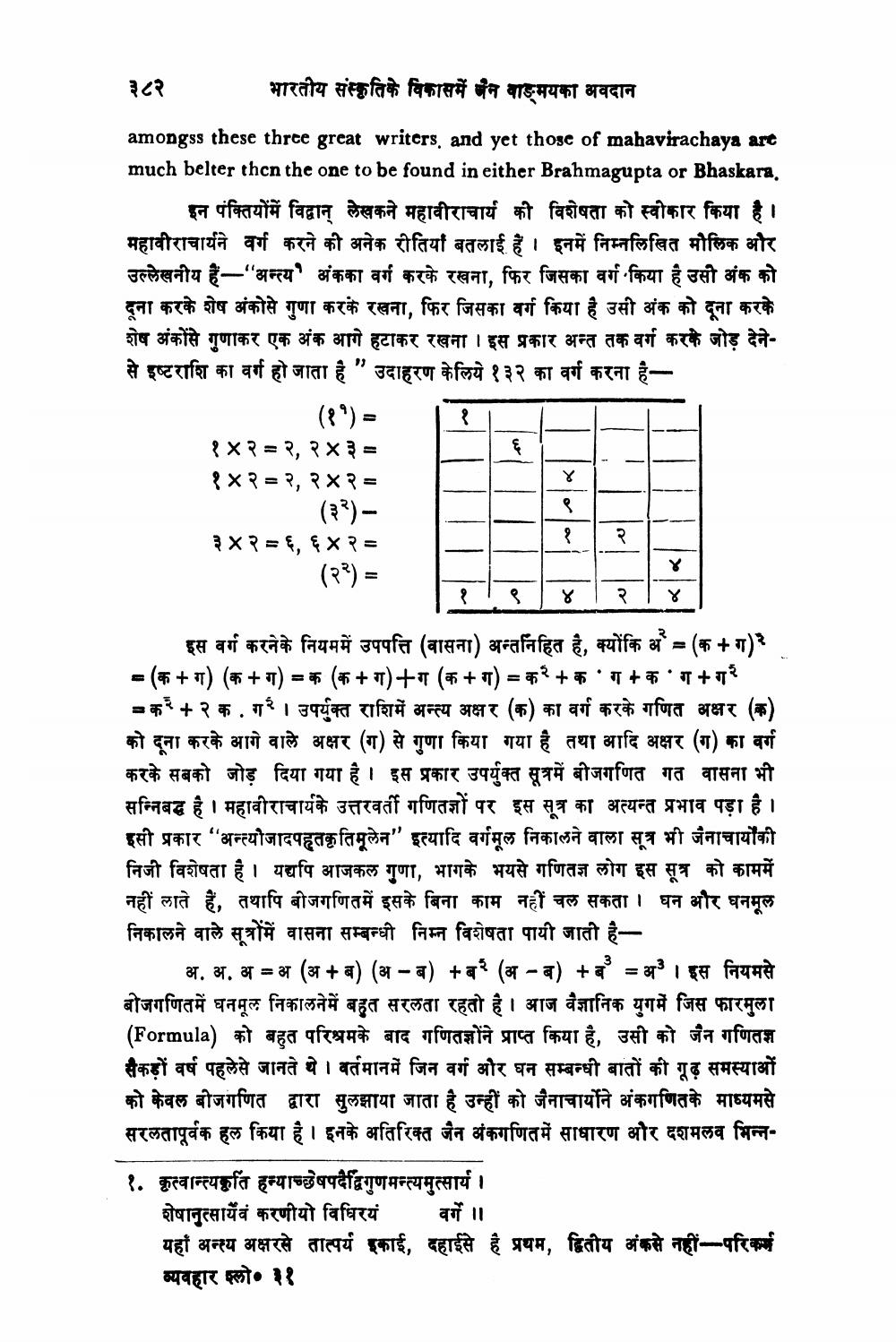
इन पंक्तियोंमें विद्वान् लेखकने महावीराचार्य की विशेषता को स्वीकार किया है। महावीराचार्यने वर्ग करने की अनेक रीतियां बतलाई है। इनमें निम्नलिखित मौलिक और उल्लेखनीय हैं-"अन्त्य' अंकका वर्ग करके रखना, फिर जिसका वर्ग किया है उसी अंक को दूना करके शेष अंकोसे गुणा करके रखना, फिर जिसका वर्ग किया है उसी अंक को दूना करके शेष अंकोंसे गुणाकर एक अंक आगे हटाकर रखना । इस प्रकार अन्त तक वर्ग करके जोड़ देनेसे इष्टराशि का वर्ग हो जाता है " उदाहरण केलिये १३२ का वर्ग करना है
१४२ = २, २४३ = १४२ = २,२४२ =
(३२)३४२ = ६,६
(२२) =
इस वर्ग करने के नियममें उपपत्ति (वासना) अन्तनिहित है, क्योंकि मैं = (क + ग)२ . = (क + ग) (क + ग) = क (क + ग)+ग (क + ग) = क + क ग + क ग + गई। = क + २ क . गरे । उपर्युक्त राशिमें अन्त्य अक्षर (क) का वर्ग करके गणित अक्षर (क) को दूना करके आगे वाले अक्षर (ग) से गुणा किया गया है तथा आदि अक्षर (ग) का वर्ग करके सबको जोड़ दिया गया है । इस प्रकार उपर्युक्त सूत्रमें बीजगणित गत वासना भी सन्निबद्ध है । महावीराचार्य के उत्तरवर्ती गणितज्ञों पर इस सूत्र का अत्यन्त प्रभाव पड़ा है। इसी प्रकार "अन्त्यौजादपहृतकृतिमूलेन" इत्यादि वर्गमूल निकालने वाला सूत्र भी जैनाचार्योकी निजी विशेषता है । यद्यपि आजकल गुणा, भागके भयसे गणितज्ञ लोग इस सूत्र को काममें नहीं लाते हैं, तथापि बीजगणितमें इसके बिना काम नहीं चल सकता। घन और घनमूल निकालने वाले सूत्रोंमें वासना सम्बन्धी निम्न विशेषता पायी जाती है
अ. अ. अ = अ (अ + ब) (अ - ब) + ब (अ - ब) + 2 = अ । इस नियमसे बोजगणितमें घनमूल निकालनेमें बहुत सरलता रहती है। आज वैज्ञानिक युगमें जिस फारमुला (Formula) को बहुत परिश्रमके बाद गणितज्ञोंने प्राप्त किया है, उसी को जैन गणितज्ञ सैकड़ों वर्ष पहलेसे जानते थे । वर्तमानमें जिन वर्ग और घन सम्बन्धी बातों की गूढ़ समस्याओं को केवल बीजगणित द्वारा सुलझाया जाता है उन्हीं को जैनाचार्योने अंकगणितके माध्यमसे सरलतापूर्वक हल किया है । इनके अतिरिक्त जैन अंकगणितमें साधारण और दशमलव भिन्न१. कृत्वान्त्यकृति हन्याच्छेषपदैद्विगुणमन्त्यमुत्सार्य ।
शेषानुत्सायेवं करणीयो विधिरयं वर्गे । यहाँ अन्त्य अक्षरसे तात्पर्य इकाई, दहाईसे है प्रथम, द्वितीय अंकसे नहीं-परिकर्म व्यवहार श्लो. ३१