Shekharchandra Jain Abhinandan Granth Smrutiyo ke Vatayan Se

SR No.: 012084
Original Sutra Author: N/A
Author: Shekharchandra Jain Abhinandan Samiti
Publisher: Shekharchandra Jain Abhinandan Samiti
Publication Year: 2007
Total Pages: 580
Language: Hindi
Classification: Smruti_Granth
File Size: 21 MB

Page 409

तिथि
१०
1364 1364
स्मृतियों के वातायन से । सम्मत और जैनमान्यता की ध्रुवराशि पर विचार करने से स्पष्ट है कि नक्षत्रात्मक ध्रुवराशिका उत्तरकालीन राशि के विकास में महत्त्वपूर्ण योग है। आगे इसी प्रक्रिया का विकसित रूप क्रान्तिवृत्त के द्वादशभागात्मक राशि है। __पञ्चवर्षात्मक युग में जैनाचार्यों की व्यतीपात-आनयानसम्बन्धी पक्रिया का उत्तरकालीन भारतीय ज्योतिष में महत्त्वपूर्ण स्थान है। ज्योतिष करण्डकी निम्न गाथाओं में इस प्रक्रिया का विवेचन मिलता है।'
अयणाणं सम्बन्ये रविसोमाणं तु वे हि य जुगम्मि। जं हवइ भागलबं वइहया तत्तिया होन्ति॥ वावत्ततरीपमाणे फलरासी इच्छिते उ जुगभेए।
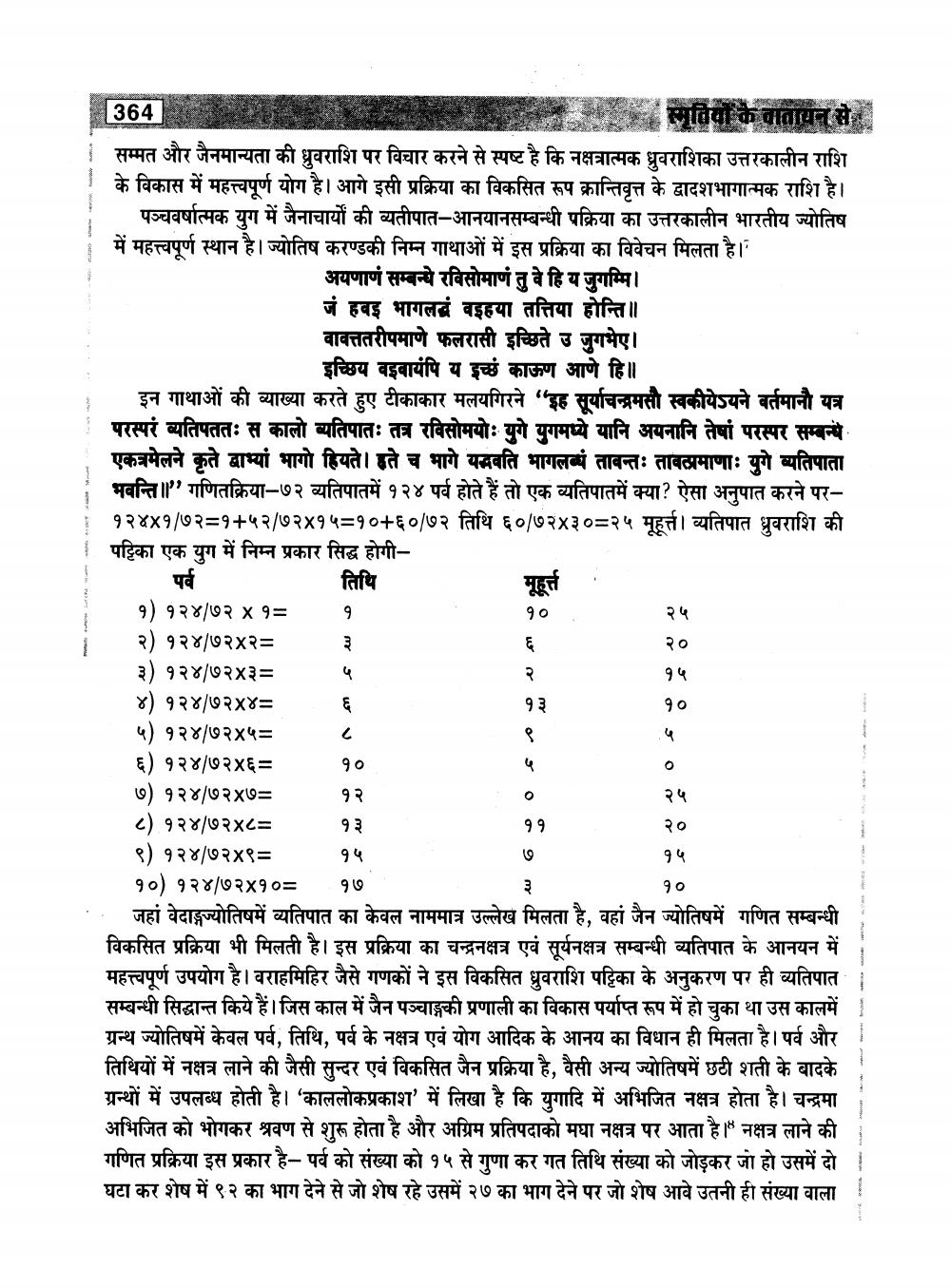
इच्छिय वइबायंपि य इच्छं काऊण आणे हि॥ इन गाथाओं की व्याख्या करते हुए टीकाकार मलयगिरने "इह सूर्याचन्द्रमसौ स्वकीयेऽयने वर्तमानौ यत्र परस्परं व्यतिपततः स कालो व्यतिपातः तत्र रविसोमयोः युगे युगमध्ये यानि अयनानि तेषां परस्पर सम्बन्ध एकत्रमेलने कृते बाभ्यां भागो हियते। हृते च भागे यनवति भागलबं तावन्तः तावठामाणाः युगे व्यतिपाता भवन्ति॥" गणितक्रिया-७२ व्यतिपातमें १२४ पर्व होते हैं तो एक व्यतिपातमें क्या? ऐसा अनुपात करने पर१२४४१/७२=१+५२/७२४१५=१०+६०/७२ तिथि ६०/७२४३०=२५ मूहूर्त। व्यतिपात ध्रुवराशि की पट्टिका एक युग में निम्न प्रकार सिद्ध होगी
पर्व १) १२४/७२ x १= १ २) १२४/७२x२= ३) १२४/७२४३= ४) १२४/७२४४= ५) १२४/७२४५= ६) १२४/७२x६= ७) १२४/७२४७= ८) १२४/७२४८= ९) १२४/७२४९% १०) १२४/७२४१०= .
जहां वेदाङ्गज्योतिषमें व्यतिपात का केवल नाममात्र उल्लेख मिलता है, वहां जैन ज्योतिषमें गणित सम्बन्धी विकसित प्रक्रिया भी मिलती है। इस प्रक्रिया का चन्द्रनक्षत्र एवं सूर्यनक्षत्र सम्बन्धी व्यतिपात के आनयन में महत्त्वपूर्ण उपयोग है। वराहमिहिर जैसे गणकों ने इस विकसित ध्रुवराशि पट्टिका के अनुकरण पर ही व्यतिपात सम्बन्धी सिद्धान्त किये हैं। जिस काल में जैन पञ्चाङ्गकी प्रणाली का विकास पर्याप्त रूप में हो चुका था उस कालमें ग्रन्थ ज्योतिषमें केवल पर्व, तिथि, पर्व के नक्षत्र एवं योग आदिक के आनय का विधान ही मिलता है। पर्व और तिथियों में नक्षत्र लाने की जैसी सुन्दर एवं विकसित जैन प्रक्रिया है, वैसी अन्य ज्योतिषमें छठी शती के बादके ग्रन्थों में उपलब्ध होती है। 'काललोकप्रकाश' में लिखा है कि युगादि में अभिजित नक्षत्र होता है। चन्द्रमा अभिजित को भोगकर श्रवण से शुरू होता है और अग्रिम प्रतिपदाको मघा नक्षत्र पर आता है। नक्षत्र लाने की गणित प्रक्रिया इस प्रकार है- पर्व को संख्या को १५ से गुणा कर गत तिथि संख्या को जोड़कर जो हो उसमें दो घटा कर शेष में ९२ का भाग देने से जो शेष रहे उसमें २७ का भाग देने पर जो शेष आवे उतनी ही संख्या वाला
ur r
" -
0
9
m