Arhat Vachan 2002 01

SR No.: 526553
Original Sutra Author: N/A
Author: Anupam Jain
Publisher: Kundkund Gyanpith Indore
Publication Year: 2002
Total Pages: 108
Language: Hindi
Classification: Magazine, India_Arhat Vachan, & India
File Size: 7 MB

Page 14

A = 10.212
............ (18) and implies the usual 'accurate' Jaina value n = 10. The corresponding vyāvahārika rule, for the area of a bow - figure, based on the simple practical value r = 3 will be A = 3 c.h/4
.... ..... (19) which is not found in the mentioned works of Mahavira and Nemicandra. Thus we find that for the area of a bow - figure two apparently different type of rules were used by the Jainas. A comparison of the three rules (13), (15) and (19) along with A = n ch/4 (with true )
............. (20) and the modern exact area Ao = (0 - sino.coso)
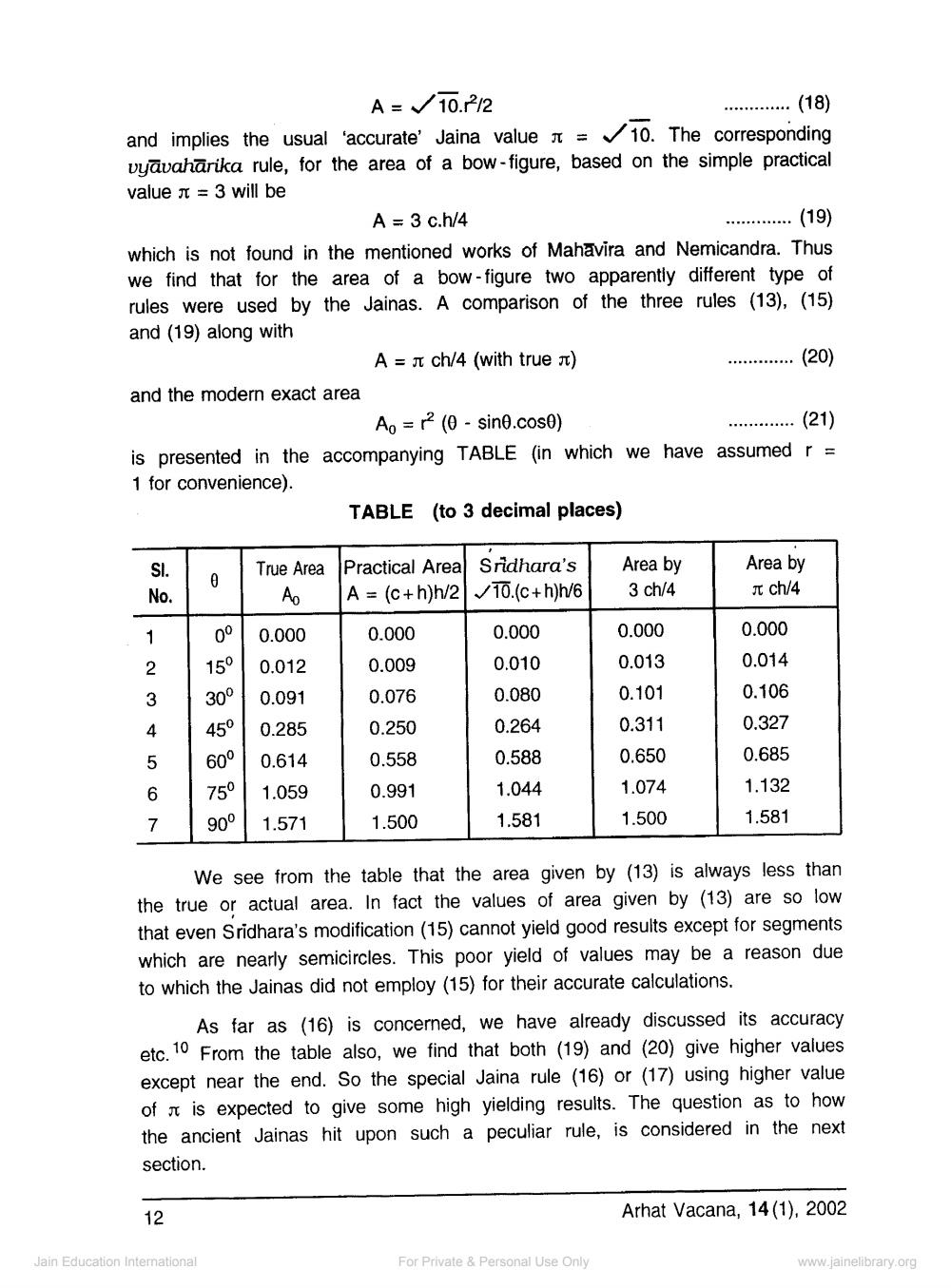
............ (21) is presented in the accompanying TABLE (in which we have assumed r = 1 for convenience).
TABLE (to 3 decimal places)
A
SI. No.
True Area Practical Area Sridhara's True A A = (c+h)h/
2 17.(c+h)h/6
Area by 3 ch/4
Area by I ch/4
А.
0.000
0.014 0.106
30°
45° |
0.000 0.012 0.091 0.285 0.614 1.059 1.571
0.000 0.009 0.076 0.250 0.558 0.991 1.500
0.000 0.010 0.080 0.264 0.588 1.044 1.581
0.000 0.013 0.101 0.311 0.650 1.074 1.500
0.327
0.685 1.132 1.581
90°
We see from the table that the area given by (13) is always less than the true or actual area. In fact the values of area given by (13) are so low that even Sridhara's modification (15) cannot yield good results except for segments which are nearly semicircles. This poor yield of values may be a reason due to which the Jainas did not employ (15) for their accurate calculations.
As far as (16) is concerned, we have already discussed its accuracy etc. 10 From the table also, we find that both (19) and (20) give higher values except near the end. So the special Jaina rule (16) or (17) using higher value of r is expected to give some high yielding results. The question as to how the ancient Jainas hit upon such a peculiar rule, is considered in the next section.
12
Arhat Vacana, 14(1), 2002