Ganitasara Sangraha

SR No.: 020800
Original Sutra Author: N/A
Author: Mahaviracharya, M Rangacharya
Publisher: Government of Madras
Publication Year: 1912
Total Pages: 523
Language: Hindi, Sanskrit
Classification: Book_Devnagari
File Size: 22 MB

Page 410

CHAPTER VII-MEASUREMENT OF AREAS.
213
figure ; and the measure of the base (of either of the derived figures of reference) happens to be the measure of the perpendicular (dropped to the base from either of the end-points of the topside in the required figure).
An example in illustration thereof. 1001. In relation to a quadrilateral with two equal sides constructed with the aid of 5 and 6 as bējas give out the measures of the top side, of the base, of (either of the two equal) sides, of the perpendicular (from the top to the base), of the diagonal), of the lesser) segmeat (of the base), and of the area.
The rule for arriving at the measures of the top-side, of the base, of any one of) the (equal) sides, of the perpendicular (from the top to the base), of the diagonal, of the (lesser) segment (of the base) and of the area, in relation to a quadrilateral having three equal sides (with the aid of given bijas) :
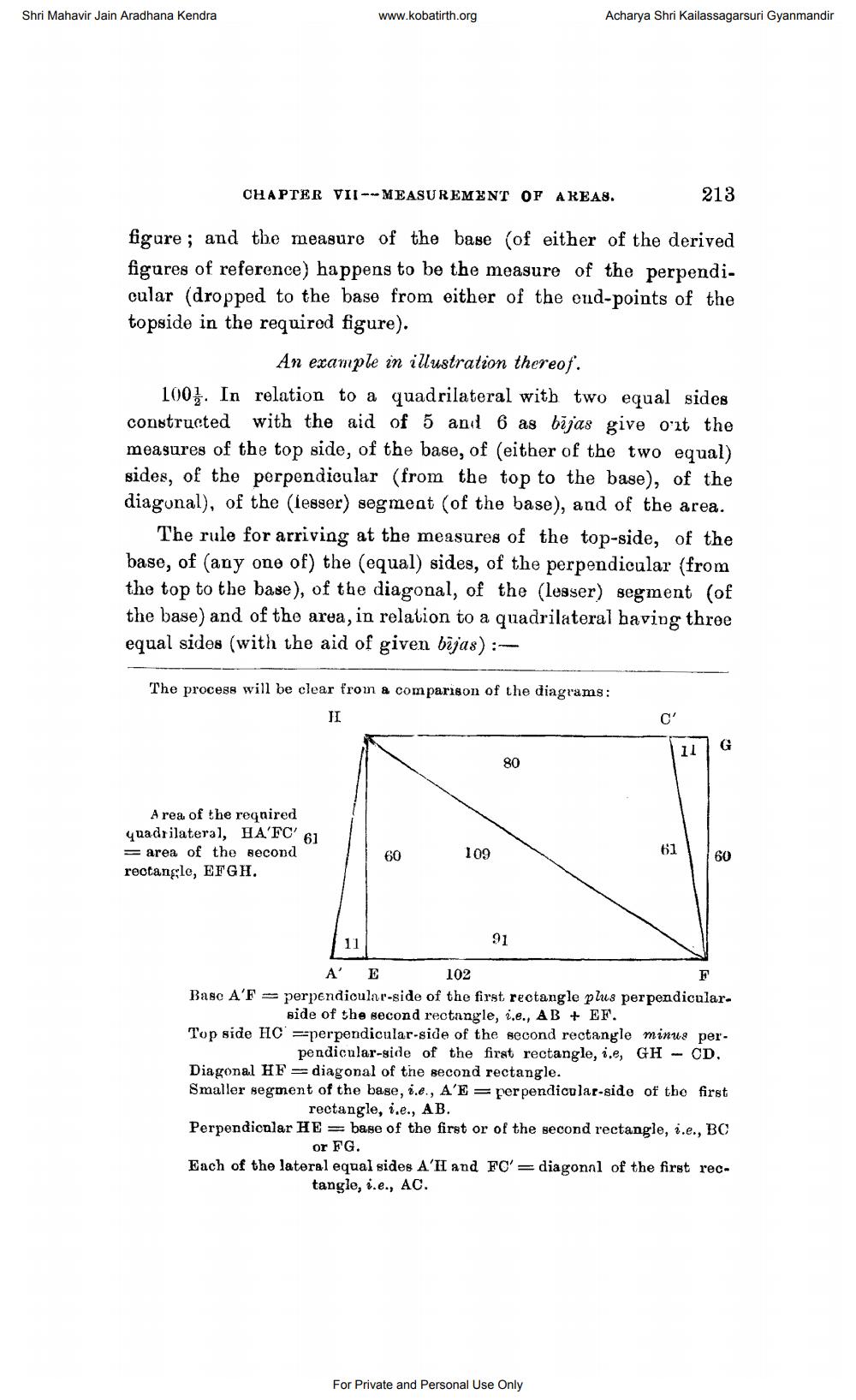
The process will be clear from a comparison of the diagrams:
I
G
111
80
Area of the reqnired quadrilateral, HAFC' 61 = area of the second 160109 rectangle, EFGH.
61
60
A' E 102 Basc AF = perpendicular-side of the first rectangle plus perpendicular
side of the second rectangle, i.e., AB + EF. Top side HC =perpendicular-side of the second rectangle minua per
pendicular-side of the first rectangle, i.e, GH - CD. Diagonal HF = diagonal of the second rectangle. Smaller segment of the base, 6.e., A'E= perpendicular-side of the first
rectangle, i.e., AB. Perpendicular HE= base of the first or of the second rectangle, i.e., BC
or FG. Each of the lateral equal sides A'H and FC'= diagonal of the first rec
tangle, i.e., AC.