Tulsi Prajna 1997 10

SR No.: 524593
Original Sutra Author: N/A
Author: Parmeshwar Solanki
Publisher: Jain Vishva Bharati
Publication Year: 1997
Total Pages: 188
Language: Hindi
Classification: Magazine, India_Tulsi Prajna, & India
File Size: 8 MB

Page 141

Vol. XXIII, No.3
107 Nemicandra gave the following Gatha to find the total number of the letters of scriptural knowledge.
___चउसट्ठिपदं विरलिय दुगं च दाऊण संगुणं किच्चा ।
रूऊण च कुए पुण सुदणाणस्सक्खरा होति ।।10 This Gatha means to make 64 places and put down 2 on every one, then multiply all the twos with eachother. Subtract I from the total multiplication to find the total number of the letters of scriptural knowledge. Numerically it is;
2 x 2 x 2 x ----64 times-1 or 264-1 This method can be generalised as follows.
If n is the numb:r of objects then the total number of all possible combinations without taking permutations into account is;
2 x 2 x 2 ----- n times-1 or 20-1
When the real method is out of approach, such mathematical model is the best alternative. Such self working system makes mathematics simple and easy for laymen and gives aid to the computer-programming
To know what type of mathematics is used in the above working system, there exists two possibilities. Both of them take us into the light of mathematics used in general and the second gives emphasis on why it is in the form of 20-1 in particular. (4.1) Mathematics of G.P. with combination :
This possibility is traditionally very well known.
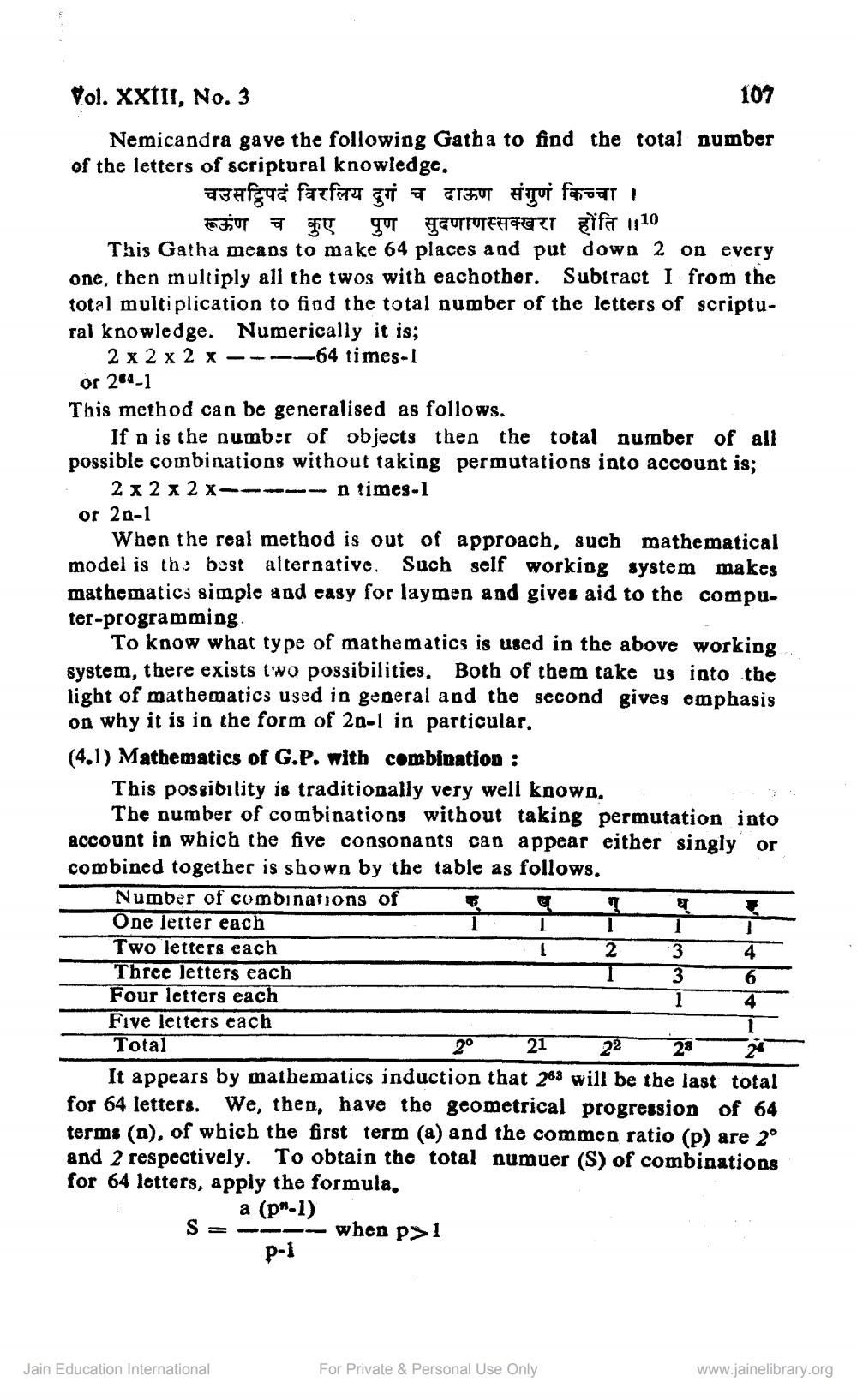
The number of combinations without taking permutation into account in which the five consonants can appear either singly or combined together is shown by the table as follows.
Number of combinations of One letter each Two letters each Three letters each Four letters each Five letters cach Total
2° 21 22 2821 It appears by mathematics induction that 268 will be the last total for 64 letters. We, then, have the geometrical progression of 64 terms (a), of which the first term (a) and the common ratio (p) are 2° and 2 respectively. To obtain the total numuer (S) of combinations for 64 letters, apply the formula.
a (pm-1) S=- - when ps1
P-1